JPEG Image Compression: What you don't see (pt. I)
Text Size VS Image size: Who's bigger?
Remember the article that you read before starting this one. What was it about? Did you like it? There were some images in it for sure. So, if sum up all the text from that article and then look at the size of just one single image of the very same article - will the text size be bigger? No, of course, and that's right time for the image compression algorithms to shine.
We do know that image sizes are typically larger than text files. That's due to amount of information any image may contain - algorithm must save all of those pixel data and later the browser will transmit them to your device. So, if an image is big, and we mean, really big, like 4 mb - it doesn't help download speed, does it now? Here at Compressman's Team, we study how to ensure quite the opposite. Images must be presented in some compact format, to help download speed and don't hurt image quality.
Here we took a glance at JPEG image representation; at how does image file use just a bit of computer memory to get things done. Later we will dive into some mathematical mumbo-jumbo to understand JPEG 2000 standard a little bit better.
Image Representation Matters
The very theme - which is basically data compression - of our article asks one ultimate question. It sounds like this: "How on earth can we represent information in a compact, all-suitable way?" Not just images - and videos, text and music files also. There is a need to compress data across all mediums. Thanks to compression, you can listen to thousands songs with your device, watch movies and store myriads of pictures.
But how doesn one actually compress data? The answer is to cut here and there: to organize the information in such way that allows to erase all redundant parts. But let's go closer to our topic, closer to image compression algorithms discussion. Here we will examine JPEG baseline compression method. We will use this image as an example. By the way, JPEG is an acronym for "Joint Photographic Experts Group." in case you didn't know. This format is not lossless, meaning id does not preserve all original information (lossless stands for no losses, y'a know). JPEG baseline algorithm is in fact lossy -it does lose some information, but only if it is unimportant.
Fine, but how many bytes do we need for this image to be? Let's count at least approximately.
- This image's pixels are arranged in a rectangular grid. Dimensions are 250 by 375 - it gives us total of 93,750 pixels.
- The colour of each pixel is determined by the amount of red, green and blue colours being mixed together. Each colour channel has a value range of 256 (from 0 to 256). This means that one colour requires one byte of computer memory. We have not one, but three colours, so we need three bytes for one pixel.
93,750*3 = 281,250 bytes
However, the JPEG image shown here is only 32,414 bytes. In other words, the image has been compressed by a factor of roughly nine. Quite a result, one might say. We will describe how the image can be represented in such a small file (compressed) and how it may be reconstructed (decompressed) from this file.
The Ways of JPEG Image Compression Algorithm
First of all, the image is divided into 8-by-8 blocks of pixels.

As we can see, image compression algorithm is processing each block without reference to the other ones. We will concentrate on a single block. In fact, we will focus on the block highlighted below.

Here is the same block blown up so that the individual pixels are more apparent. See how there is not noticable variation over the 8-by-8 block (but do remember, that other blocks may have more diversity).

Do not forget the main goal of image compression algorithm. It needs to represent given data in some way that shows some redundancy. Each and every pixel color is a representation of a three-dimensional vector (RGB, which stands for Red, Green, Blue). This vector consists of its red, green, and blue components variables. If you take any image, you will see that there is a lot of dependency between these three variables.This is the reason why we will use a colour space transform to create a new vector whose components represent luminance, Y, blue and red chrominance, Cb and Cr.
Chrominance is a colorimetric difference between a given colour in a television picture and a standard colour of equal luminance.

The luminance variable is basically the brightness of the given pixel. It allows us to see grades of any colour. The chrominance information tells us about colour's hue. Commonly these three variables are much less correlated than the (R, G, B) variables. Hence, visual studies show us that the oureye is much more sensitive to luminance than chrominance. This means that we can neglect big changes in the chrominance without affecting our vision of the image during the image compression process. Do not worry - this change can be Supermaned. Got it?

So we can undo the changes. That is why we will be able to recreate the (R,G,B) vector from the (Y, Cb, Cr) vector. This part will be pretty important since we want to reconstruct the image. (Let us add even more: as usual, we add 128 to the chrominance variables so that we represent them as numbers between 0 and 255 anyway.)
OK, so now all we need to do is to use this change gor each and every pixel in our block; one to each variable. Take a look at the images below. Notice how brighter pixels change to larger, much larger values.




Let's discuss this result of image compression process. The luminance gives much more differente pixels than the chrominance. This is the reason why the best compression ratios are often achieved by deciding that chrominance values are constant on 2-by-2 blocks. As the following, less of these values will be recorded. For example, the image editing software Gimp has the this kind of menu when saving an image as a JPEG file: IMAGE Note: The "Subsampling" option gives us an option to choose between various ways of subsampling the chrominance values. We will talk about the "Quality" option a bit late, but trust us - it is important as well.
The Discrete Cosine Transform Image Compression
Now we come to the heart of our image compression calculation. What we want is that, over an 8 by 8 piece, the changes in the components of the (Y, Cb, Cr) vector are maybe gentle, as illustrated by the example we have just seen. Instead of recording the specific values of the components, we could record, say, the normal values and how much each pixel varies from this normal number. In numerous cases, we would anticipate the contrasts from the normal to be maybe little and subsequently securely disregarded. This is the pith of the Discrete Cosine Change (DCT), which will now be clarified a bit more. Here's more info about that:
For a start, we will focus on one of those three components in one row in our block. Let's say, that the eight values are representations of f0, f1, ..., f7. Let's also say we want to represent these values in some specific way so that the variations become more visible, more easily noticable. So for this reason, we will represent these values as given by a function fx, where x runs from 0 to 7. Let's write this function as a linear combination of cosine functions:

You probably saw that already, but do not worry about the factor of 1/2 in front or the constants Cw (case is, that Cw = 1 for all w except C0 = 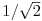 ).
).
So, what is the most important in this mathematical expression? Look no further than the function otseld. The function fx is actuallyas a linear combination of cosine functions of different frequencies with coefficients Fw. Let's take a look at these cosine functions with specific freqiencies w, using these graphs:

Deeper to the Algorithm's Core
For sure, the cosine functions in image compression algorithms with much more higher frequencies show much more fast repetitions. This is why, if the values fx change not very fast, the coefficients Fw for bigger frequencies should be quite small. Since we want to reduce the file size of our image, we can choose to not to write down those coefficients. We can found the DCT coefficients using:

Take a closer look how this implies the fact that the DCT is actually invertible. For instance, we will startwith fx and write down the values Fw. But do not forget: when we want to recreate the image, we will have the coefficients Fw and recalculate the fx.
Instead of applying the Discrete Cosine Transform Image Compression algorithm to only the rows of our blocks, we will use the two-dimensional nature of our image. Pretty smart, huh? Typically, the Discrete Cosine Transform joins its powers with the rows of a block for a start. In case the image doesn not change the very same second in the vertical direction, then the coefficients should not too. This is why we may change a value of w and apply the Discrete Cosine Transform to the eight values of Fw that we get from those eight rows. This gives us coefficients Fw,u where w is the horizontal frequency and u represents a vertical frequency.
How do we store these coeficients? Answer is simple: in another 8 by 8 block as shown in an image below.

Did you noticed that when we move down or to the right of our list, we meet coefficients corresponding to much more higher frequencies, which we think will be less significant.
The Discrete Cosine Transform Image Compression coefficients might be efficiently calculated through a Fast Discrete Cosine Transform, in the same manner that the Fast Fourier Transform efficiently computes the Discrete Fourier Transform.
End of part I. See Part II.

 By Compressman Team on 08 April, 2018
By Compressman Team on 08 April, 2018 




