Размер текста VS Размер изображения: Кто больше?

Помните статью, которую вы прочитали, прежде чем начинать ее. О чем это было? Тебе понравилось? В нем были некоторые изображения. Итак, если подвести итог всему тексту из этой статьи, а затем посмотреть размер только одного изображения той же самой статьи - будет ли размер текста больше? Нет, конечно, и сейчас самое время для сияния алгоритмов сжатия изображений.

Мы знаем, что размеры изображений обычно больше текстовых. Это связано с количеством информации, которую может содержать любое изображение. Алгоритм должен сохранять все эти данные в пикселях, а затем браузер передает их на ваше устройство. Итак, если изображение крупное, и мы имеем в виду, действительно большое, как 4 МБ - это не помогает скорости загрузки, не так ли? Здесь, в команде Compressman's, мы изучаем, как обеспечить совершенно противоположное. Изображения должны быть представлены в компактном формате, чтобы ускорить загрузку и не повредить качество изображения.

Здесь мы взглянули на представление изображения JPEG; о том, как файл изображения использует только немного памяти компьютера, чтобы все было сделано. Позже мы погрузимся в математическое mumbo-jumbo, чтобы понять стандарт JPEG 2000 немного лучше.

Представление изображений важно

Сама тема - в основном сжатие данных - нашей статьи задает один конечный вопрос. Это звучит так: «Как мы можем представить информацию в компактном, подходящем для вас способом?» Не только изображения - и видео, текстовые и музыкальные файлы. Необходимо сжимать данные во всех медиумах. Благодаря сжатию вы можете слушать тысячи песен с помощью своего устройства, смотреть фильмы и хранить мириады изображений.

Но как вообще можно сжать данные? Ответ заключается в том, чтобы разрезать здесь и там: организовать информацию таким образом, чтобы можно было удалить все избыточные части. Но давайте приблизиться к нашей теме, ближе к обсуждению алгоритмов сжатия изображений. Здесь мы рассмотрим метод сжатия базовой линии JPEG. Мы будем использовать это изображение в качестве примера. Кстати, JPEG является акронимом для «Joint Photographic Experts Group». в случае, если вы этого не знали. Этот формат не является без потерь, то есть идентификатор не сохраняет всю исходную информацию (без потерь нет потерь, вы знаете). Базовый алгоритм JPEG фактически является убыточным - он лишает некоторую информацию, но только если он неважен.

Отлично, но сколько байтов нам нужно для этого изображения? Давайте посчитаем хотя бы приблизительно.

1. Пики этого изображения расположены в прямоугольной сетке. Размеры 250 на 375 - это общее количество 93 750 пикселей.
2. Цвет каждого пикселя определяется количеством смешанных красных, зеленых и синих цветов. Каждый цветной канал имеет диапазон значений 256 (от 0 до 256). Это означает, что для одного цвета требуется один байт памяти компьютера. У нас нет ни одного, а трех цветов, поэтому нам нужно три байта для одного пикселя.

93,750 * 3 = 281,250 байт

Однако изображение JPEG, показанное здесь, составляет всего 32,414 байт. Другими словами, изображение было сжато примерно в девять раз. Вполне возможно, что можно сказать. Мы опишем, как изображение может быть представлено в таком маленьком файле (сжатом) и как оно может быть восстановлено (распаковано) из этого файла.

Способы сжатия JPEG-изображений

Прежде всего, изображение разделено на 8-на-8 блоков пикселей.

Как мы видим, алгоритм сжатия изображений обрабатывает каждый блок без ссылки на другие. Мы сосредоточимся на одном блоке. Фактически, мы сосредоточимся на блоке, выделенном ниже.

Вот тот же блок, взорванный, чтобы отдельные пиксели были более очевидными. Посмотрите, как нет заметных изменений в блоке 8 на 8 (но помните, что другие блоки могут иметь большее разнообразие).

Не забывайте о главной цели алгоритма сжатия изображений. Он должен каким-то образом представлять данные, которые показывают некоторую избыточность. Каждый пиксельный цвет представляет собой представление трехмерного вектора (RGB, который обозначает красный, зеленый, синий). Этот вектор состоит из переменных красного, зеленого и синего компонентов. Если вы возьмете какое-либо изображение, вы увидите, что между этими тремя переменными существует большая зависимость. Именно поэтому мы будем использовать преобразование цветового пространства для создания нового вектора, компоненты которого представляют яркость, Y, синий и красный цветность, Cb и Cr.

Chrominance - это колориметрическая разница между заданным цветом в телевизионном изображении и стандартным цветом равной яркости.

Переменная яркости - это в основном яркость данного пикселя. Это позволяет нам видеть оценки любого цвета. Информация о цветности сообщает нам о цвете оттенка. Обычно эти три переменные гораздо менее коррелируют, чем переменные (R, G, B). Следовательно, визуальные исследования показывают нам, что oureye гораздо более чувствительны к яркости, чем цветность. Это означает, что мы можем пренебрегать большими изменениями в цветности, не влияя на наше видение изображения во время процесса сжатия изображения. Не беспокойтесь - это изменение может быть отсуперменены. Смекнули?

Таким образом, мы можем отменить изменения. Вот почему мы сможем воссоздать вектор (R, G, B) из вектора (Y, Cb, Cr). Эта часть будет очень важной, так как мы хотим восстановить изображение. (Добавим еще больше: как обычно, добавим 128 к переменным цветности, чтобы мы представляли их как числа от 0 до 255 в любом случае.)

Хорошо, так что теперь все, что нам нужно сделать, это использовать это изменение gor каждый пиксель в нашем блоке; по одной на каждую переменную. Взгляните на приведенные ниже изображения. Обратите внимание на то, как более яркие пиксели меняются на большие, гораздо более крупные значения.

Давайте обсудим этот результат процесса сжатия изображения. Яркость дает гораздо больше разных пикселей, чем цветность. Именно по этой причине наилучшие коэффициенты сжатия часто достигаются путем определения того, что значения цветности являются постоянными на блоках 2 на 2. Как указано ниже, будет записано меньше этих значений. Например, программное обеспечение для редактирования изображений Gimp имеет такое меню при сохранении изображения в виде файла JPEG: IMAGE Примечание. Опция «Subsampling» дает нам возможность выбирать между различными способами подвыборки значений цветности. Мы немного поговорим о варианте «Качество», но будем доверять нам - это тоже важно.

Сжатие изображения с дискретным косинусным преобразованием

Теперь мы находимся в основе нашего расчета сжатия изображений. Мы хотим, чтобы изменения в компонентах вектора (Y, Cb, Cr) на 8-8 единиц были незначительными, как показано на примере, который мы только что видели. Вместо того, чтобы записывать конкретные значения компонентов, мы могли бы записывать, скажем, нормальные значения и то, как каждый пиксель изменяется от этого нормального числа. Во многих случаях мы ожидали бы, что контрасты от нормального могут быть немногочисленными и впоследствии безопасно проигнорированы. Это суть дискретного косинусного изменения (DCT), который теперь будет уточнен еще немного. Подробнее об этом:

Для начала мы сосредоточимся на одном из этих трех компонентов в одной строке нашего блока. Предположим, что восемь значений представляют собой представления f0, f1, ..., f7. Давайте также скажем, что мы хотим представить эти значения каким-то определенным образом, чтобы изменения стали более заметными, более легко заметными. Поэтому по этой причине мы будем представлять эти значения, заданные функцией fx, где x пробегает от 0 до 7. Запишем эту функцию как линейную комбинацию косинусных функций:

Вы, наверное, уже это видели, но не беспокойтесь о коэффициенте 1/2 спереди или константах Cw (случай, что Cw = 1 для всех w, кроме C0 = ).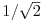

Итак, что является самым важным в этом математическом выражении? Посмотрите не дальше функции otseld. Функция fx фактически является линейной комбинацией косинусных функций разных частот с коэффициентами Fw. Давайте посмотрим на эти косинусные функции с определенными частотами w, используя эти графики:

Углубление ядра алгоритма

Конечно, функции косинуса в алгоритмах сжатия изображений с гораздо более высокими частотами показывают гораздо более быстрые повторения. Поэтому, если значения fx меняются не очень быстро, коэффициенты Fw для больших частот должны быть весьма малыми. Поскольку мы хотим уменьшить размер файла нашего изображения, мы можем не записывать эти коэффициенты. Мы можем найти коэффициенты DCT, используя:

Поразмыслите, как это подразумевает тот факт, что DCT фактически обратим. Например, мы начнем с fx и запишем значения Fw. Но не забывайте: когда мы хотим воссоздать образ, мы получим коэффициенты Fw и пересчитаем fx.

Вместо применения алгоритма сжатия дискретного косинусного преобразования изображения только к строкам наших блоков мы будем использовать двумерный характер нашего изображения. Довольно умный, да? Как правило, дискретное косинусное преобразование объединяет свои полномочия с строками блока для начала. Если изображение не изменит ту же самую секунду в вертикальном направлении, то коэффициенты не должны быть слишком. Вот почему мы можем изменить значение w и применить дискретное косинусное преобразование к восьми значениям Fw, которые мы получаем из этих восьми строк. Это дает нам коэффициенты Fw, u, где w - горизонтальная частота, u - вертикальная частота.

Как мы храним эти коэффициенты? Ответ прост: в другом блоке размером 8 на 8, как показано на изображении ниже.

Вы заметили, что, когда мы двигаемся вниз или справа от нашего списка, мы получаем коэффициенты, соответствующие гораздо более высоким частотам, что, по нашему мнению, будет менее значительным.

Коэффициенты сжатия дискретного косинусного преобразования могут быть эффективно рассчитаны посредством быстрого дискретного косинусного преобразования таким же образом, что быстрое преобразование Фурье эффективно вычисляет дискретное преобразование Фурье.

---

Конец первой части. См. вторую часть.

Источник: The American Mathematical Society